01月
04

哈夫曼树

发表于 • 本文总阅读数 次
字数统计: 1.2k

先说两句

  这篇博客大部分也是抄的，原文地址。

定义

  哈夫曼树，又称最优树，是一类带权路径长度最短的树。首先有几个概念需要清楚：

路径和路径长度

  从树中一个结点到另一个结点之间的分支构成两个结点的路径，路径上的分支数目叫做路径长度。树的路径长度是从树根到每一个结点的路径长度之和。

带权路径长度

  结点的带权路径长度为从该结点到树根之间的路径长度与结点上权的乘积。树的带权路径长度为树中所有叶子结点的带权路径长度之和，通常记作WPL。

  若有n个权值为w1,w2,…,wn的结点构成一棵有n个叶子结点的二叉树，则树的带权路径最小的二叉树叫做哈夫曼树或最优二叉树。

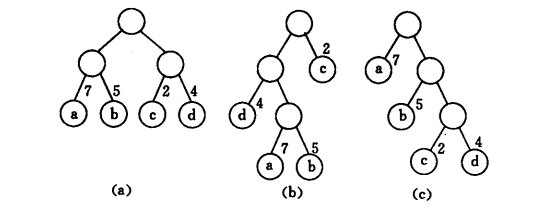
在上图中，3棵二叉树都有4个叶子结点a、b、c、d，分别带权7、5、2、4，则它们的带权路径长度为：

（a）WPL = 7×2 + 5×2 + 2×2 + 4×2 = 36
（b）WPL = 4×2 + 7×3 + 5×3 + 2×1 = 46
（c）WPL = 7×1 + 5×2 + 2×3 + 4×3 = 35

其中(c)的WPL最小，可以验证，(c)恰为哈夫曼树。

哈夫曼树的创建

  假设有n个结点，n个结点的权值分别为w1,w2,…,wn，这n个结点可以看作n个只有一个树根结点的二叉树，构成的二叉树的集合为F={T1,T2,…,Tn}。基于F，可以构造一棵含有n个叶子结点的哈夫曼树，步骤如下：

  1. 从F中选取两棵根结点权值最小的树作为左右子树构造一棵新的二叉树，其新的二叉树的权值为其左右子树根结点权值之和；
  2. 从F中删除上一步选取的两棵二叉树，将新构造的树放到F中；
  3. 重复第1步和第2步，直到F只含一棵树为止。

下面是一个构建哈夫曼树的例子：

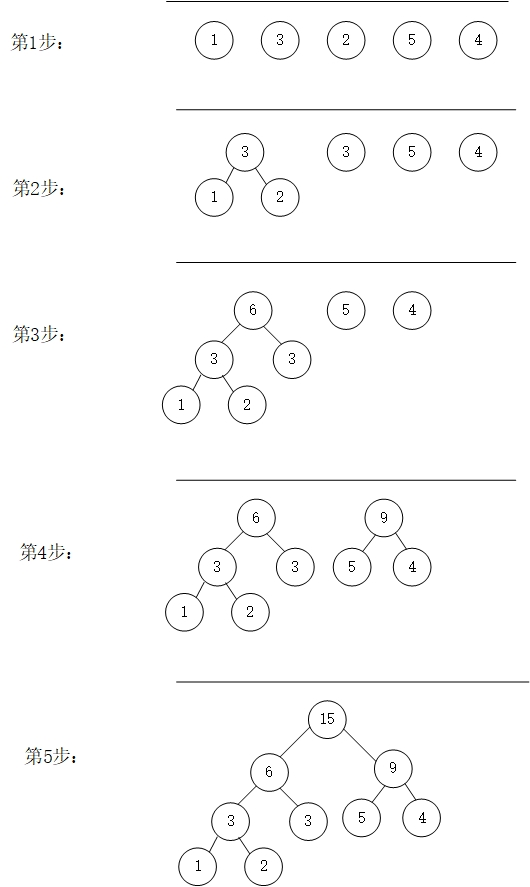
  从上面的步骤可以看出，每次都需要选取F中权值最小的两个结点，原文中，大佬用了最小堆优化查找，为了让算法简单易懂（顺便偷个懒），我就直接用数组遍历查找。

  创建哈夫曼树的C语言实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
#include <stdio.h>
#include <string.h>
#include <stdlib.h>

#define MAX_DATA_LEN 20

typedef struct tree_node
{
	char data;
	int weight;
	struct tree_node *left_child;
	struct tree_node *right_child;
} tree_node;

/**
 * @brief : 遍历结点列表，返回权重最小结点的位置
 * @param nodes : [in]结点列表
 * @param book : [in]标记数组，标记对应结点是否已经使用过
 * @param node_num : [in]结点的个数
 * @return : 权重最小结点的位置
 */
int find_min_weight_index(tree_node *nodes[], int book[], int node_num)
{
	int i, index, min_weight;

	min_weight = 0x3FFFFFFF;
	index = -1;
	for(i = 0; i < node_num; i++)
	{
		if(book[i] == 0 && nodes[i]->weight < min_weight)
		{
			index = i;
			min_weight = nodes[i]->weight;
		}
	}
	return index;
}

/**
 * @brief : 构建哈夫曼树
 * @param data_list : [in]数据数组
 * @param weight_list : [in]权重数组
 * @param data_len : [in]数据个数
 * @return : 构建好的哈夫曼树的头结点地址
 */
tree_node *build_huffman_tree(char data_list[], int weight_list[], int data_len)
{
	tree_node *nodes[MAX_DATA_LEN * 2];
	int book[MAX_DATA_LEN * 2];
	int i, node_num, index_1, index_2;

	node_num = 0;
	for(i = 0; i < data_len; i++)
	{
		nodes[i] = (tree_node *)malloc(sizeof(tree_node));
		nodes[i]->data = data_list[i];
		nodes[i]->weight = weight_list[i];
		node_num++;
	}
	memset(book, 0, sizeof(book));

	for(i = 1; i < data_len; i++)
	{
		index_1 = find_min_weight_index(nodes, book, node_num);
		book[index_1] = 1;
		index_2 = find_min_weight_index(nodes, book, node_num);
		book[index_2] = 1;
		
		nodes[node_num] = (tree_node *)malloc(sizeof(tree_node));
		nodes[node_num]->data = -1;
		nodes[node_num]->weight = nodes[index_1]->weight + nodes[index_2]->weight;
		nodes[node_num]->left_child = nodes[index_1];
		nodes[node_num]->right_child = nodes[index_2];
		node_num++;
	}
	return nodes[node_num - 1];
}

int main(int argc, char *argv[])
{
	int i, data_len = 7;
	char data_list[MAX_DATA_LEN] = {'a', 'b', 'c', 'd', 'e', 'f', 'g'};
	int weight_list[MAX_DATA_LEN] = {8, 7, 4, 5, 20, 15, 1};

	tree_node *root = build_huffman_tree(data_list, weight_list, data_len);

	return 0;
}

哈夫曼编码

  我们约定左分支表示字符`0’，右分支表示字符’1’，在哈夫曼树中从根结点开始，到叶子结点的路径上分支字符组成的字符串为该叶子结点的哈夫曼编码。上面代码所创建的哈夫曼树如下所示：

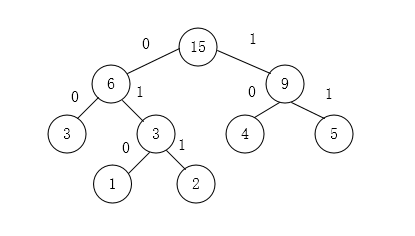
  可以看出3被编码为00，1为010，2为011,4为10,5为11。在这些编码中，任何一个字符的编码均不是另一个字符编码的前缀。

输出所有哈夫曼编码的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/**
 * @brief : 输出所有哈夫曼编码
 * @param root : [in]树根结点地址
 * @param path : [in]用来记录路径
 * @param depth : [in]当前结点的深度
 * @return : None
 */
void print_huffman_code(tree_node *root, char path[], int depth)
{
	int i;

	if(root != NULL)
	{
		if(root->data > 0)
		{
			printf("%c: ", root->data);
			for(i = 0; i < depth; i++)
			{
				printf("%d", path[i]);
			}
			printf("\n");
		}
		else
		{
			path[depth] = 0;
			print_huffman_code(root->left_child, path, depth + 1);
			path[depth] = 1;
			print_huffman_code(root->right_child, path, depth + 1);
		}
	}
}
分享到：
0%