图像的灰度变换

介绍

  灰度变换是所有图像处理技术中最简单的技术，输出图像在点$(x, y)$处的像素值仅取决于原图在点$(x, y)$处的像素值。可以用公式$s = T(r)$表示，$r$和$s$分别表示处理前后的像素值，$T$是把像素值$r$映射到像素值$s$的一种变换。
  因为处理的是数字量，所以变换函数的值通常存储在一个一维阵列里，从$r$到$s$的映射是通过查表实现的。对于8位的灰度图，$T$包含256个灰度值的映射。
  图像增强常用的三类变换函数是：线性变换、对数变换、幂律变换。

反转变换

  这个比较简单，对于一张灰度级范围为[0, L - 1]的图像，$s$就等于$L - 1 - r$，用公式表示是：$s = L - r$。
  使用这种变换方式可以反转一幅图像的灰度值，得到类似照片底片的效果。

对数变换

  对数变换的通用公式为：
$$ s = c\log(1 + r) $$

  式中$c$是常数，并假设$r>=0$。对数变换和反对数变换的曲线如下所示，蓝色曲线代表对数变换，橙色曲线代表反对数变换（图上反对数变换的公式有点看不清，是$s=e^{\frac{r}{c}} - 1$），c的取值为$\frac{L - 1}{T(L - 1)}$。对数变换将输入中范围较窄的低灰度值映射为输出中范围较宽的灰度值，将输入中范围较宽的高灰度值映射为输出中范围较窄的灰度值。使用这种类型的变换来扩展图像中的暗像素值，同时压缩更高灰度级的值。反对数变换的作用则相反。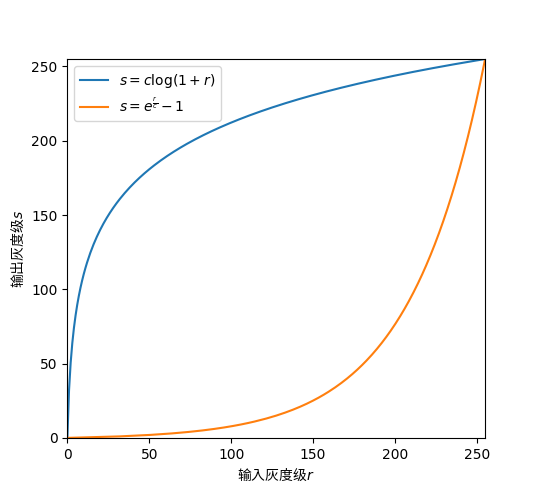

幂律变换

  幂律变换也叫伽马变换，它的通用公式为：
$$ s = cr^{\gamma} $$

  式中$c$和$\gamma$是常数。不同$\gamma$值的幂律变换曲线如下所示。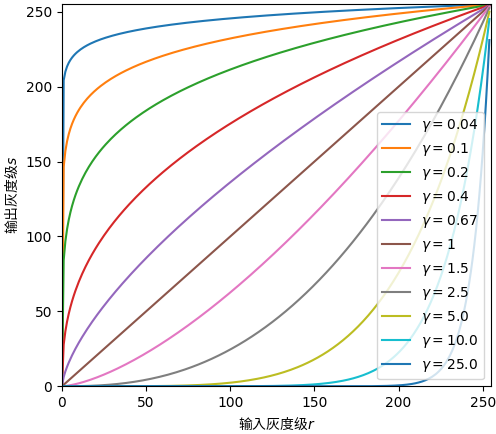

分段线性变换函数

  分段线性变换函数和名字描述的一样，就是按照不同的范围段，用线性函数进行变换。其优点是形式可以任意复杂，缺点是函数要人为调整。

对比度拉伸

  对比度拉伸是最简单的分段线性变换之一，对比度拉伸是扩展图像灰度级动态范围的处理，因此可以跨越记录介质和显示装置的全部灰度范围。下图是一个对比度拉伸的典型函数图像。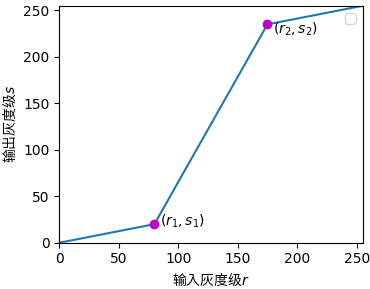

  通过变换后，灰度值在$[r_1, r_2]$范围内的像素会线性拉伸到$[s_1, s_2]$范围内，最终的结果是在范围$[r_1, r_2]$内会增强对比度，其他范围内的对比度会降低。

灰度级分层

  用于突出图像中特定范围的亮度，可以用来增强某些特征。给个书上的例图吧，不想码字了！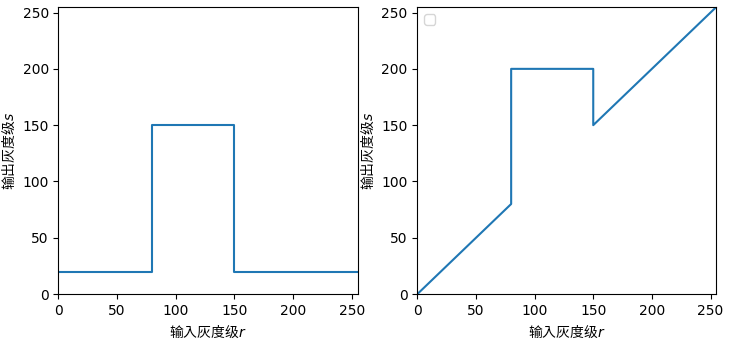

比特平面分层

  对于8比特的灰度图，每个像素由8个比特位构成，如果把图像上所有像素的特定位置的比特位单独拿出来，就可以构成一张只包含0和1的二值图像，该图像就叫原图像的比特平面。比如取每个像素中8个比特位的第7个比特位，构成该图像的第7比特平面。
  一幅图像中高位的比特平面包含了视觉上很重要的大多数数据，低位的比特平面则展现了图像更精细的灰度细节。