02月
23

HDU-1067 Gap

发表于 • 本文总阅读数 次
字数统计: 712

广度优先搜索＋map标记状态

题目

http://acm.hdu.edu.cn/showproblem.php?pid=1067

题意

  首先给出28（4×7）张卡片和一个4×8的表格，每张卡片都有一个数字，分别是11～17、21～27、31～37和41～47。初始时将卡片随机放入表格里除第一列以外的其他位置，如下图：

然后将数字11的卡片放到第一列的第一行，数字21的卡片放到第一列的第二行，数字31和41的卡片类似，如下图：

接下来需要移动卡片，移动的规则是，只能将卡片移动到空白格子上，且移动到空白格子上的卡片，必须是比空白格子左边卡片上的数字大1的那张。比如上图的第一行的第二列空白格子，其左边卡片上的数字是42，那么只能将数字为43的卡片移动到该空白格子上。在移动过若干次卡片后，如果卡片的位置能变成下图所示的样子，输出最小移动的次数，否则输出-1。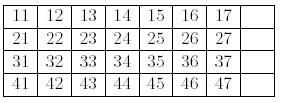

解题思路

  这题要计算最小移动的次数，首先想到的是用广度优先搜索，比较麻烦的是标记每次移动后状态。可以将表格的状态转化为一个长度为28的字符串（4×7，表格第一列不会被移动，所以不用标记），然后用map的这个字符串来判断该状态是否被标记过。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
#include <stdio.h>
#include <string.h>
#include <string>
#include <queue>
#include <map>

using namespace std;

typedef struct node
{
	char index[4];
	char a[30];
	int t;
} node;

int solve(node start)
{
	int i, j, k, si, di, dnum;
	node tep;
	queue<node> que;
	map<string, bool> mp;
	char end[30] = 
	{
		12, 13, 14, 15, 16, 17, 1,
		22, 23, 24, 25, 26, 27, 1,
		32, 33, 34, 35, 36, 37, 1,
		42, 43, 44, 45, 46, 47, 1, 0
	};

	if(strcmp(start.a, end) == 0)
	{
		return 0;
	}
	que.push(start);
	mp[start.a] = true;
	while(que.empty() == false)
	{
		for(k = 0; k < 4; k++)
		{
			tep = que.front();
			si = tep.index[k];
			dnum = (si % 7 == 0) ? si / 7 * 10 + 12 : tep.a[si - 1] + 1;
			if(dnum == 2 || dnum % 10 == 8)
			{
				continue;
			}
			for(i = 0; i < 28; i++)
			{
				if(tep.a[i] == dnum)
				{
					di = i;
					break;
				}
			}
			tep.a[di] = 1;
			tep.a[si] = dnum;
			tep.index[k] = di;
			tep.t++;
			if(strcmp(tep.a, end) == 0)
			{
				return tep.t;
			}
			if(mp.count(tep.a) == 1)
			{
				continue;
			}
			mp[tep.a] = true;
			que.push(tep);
		}
		que.pop();
	}
	return -1;
}

int main()
{
	int n, i, j, k, ans, in;
	node start;
	
	scanf("%d", &n);
	while(n--)
	{
		k = 0;
		for(i = 0; i < 4; i++)
		{
			for(j = 0; j < 7; j++)
			{
				scanf("%d", &in);
				start.a[i * 7 + j] = (char)in;
				if(start.a[i * 7 + j] % 10 == 1)
				{
					start.a[i * 7 + j] = 1;
					start.index[k] = i * 7 + j;
					k++;
				}
			}
		}
		start.a[28] = '\0';
		start.t = 0;
		ans = solve(start);
		printf("%d\n", ans);
	}
	return 0;
}
分享到：
0%